Asymmetric Laplace Distribution

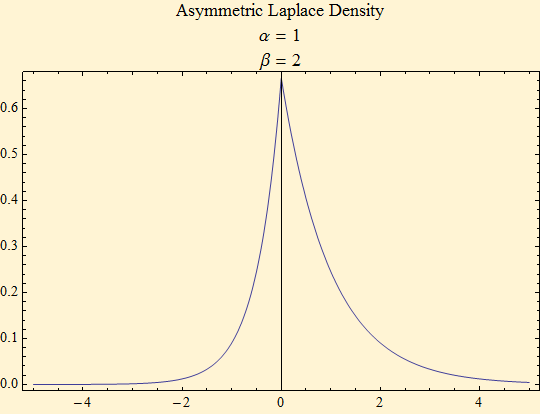
In this section we develop an asymmetric Laplace distribution from the difference of two exponential random variables.  The exponent of this random variable leads to a double Pareto distribution.  For papers on this subject follow the path to William Reed on the reference page.  Mathematica provides a symmetric Laplace distribution (essentially a double exponential distribution).  If we take the distribution of the difference of two exponential random variables with different scale factors we can generate the asymmetric Laplace distribution.  The distribution's characteristic function can be written as the product of two exponential characteristic functions.  α and β are scale factors with α > 0 && β > 0.

The density of this distribution is:

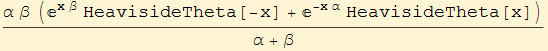
The distribution function becomes:

Note that in the references you will find the asymmetric Laplace distribution defined piecewise.  This density function has the same characteristic function

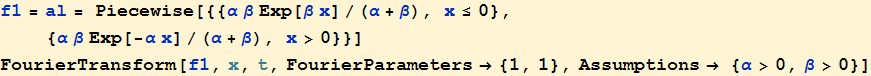
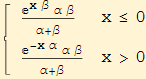
Normal Laplace Distribution

We now derive the Normal Laplace distribution as a convolution of normal and asymmetric Laplace random variables.  Theoretically we ought to be able to invert the product of the normal characteristic function and the asymmetric Laplace function, but Mathematica can't seem to do this.  It can, however, do the convolution.

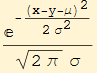
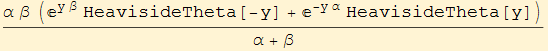
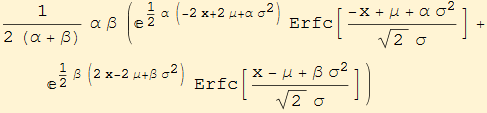
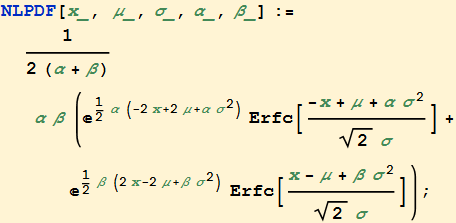
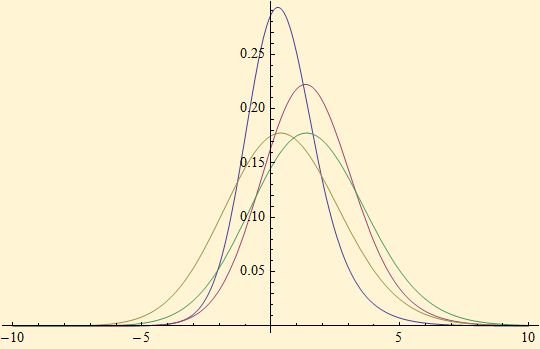
The distribution function is:

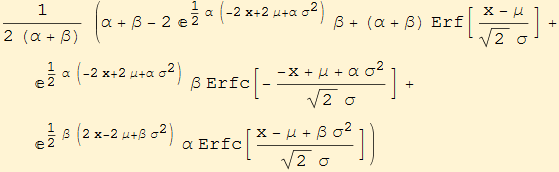
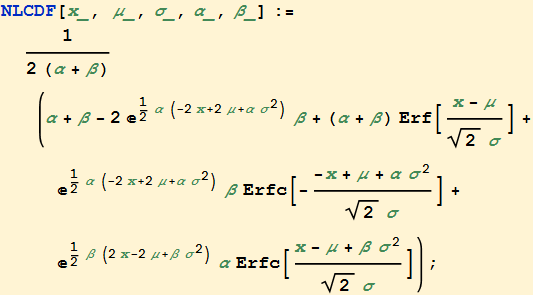
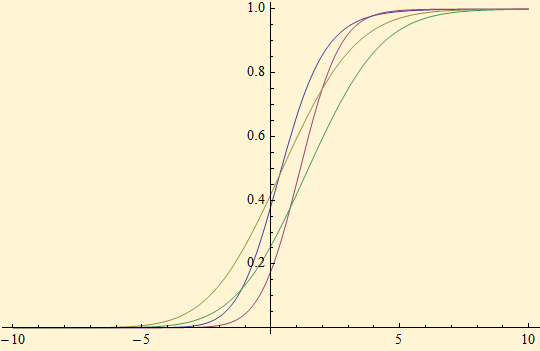
Random variables for this distribution can be generated simply enough as the sum of a normal random variable with the difference of two exponential random variables.

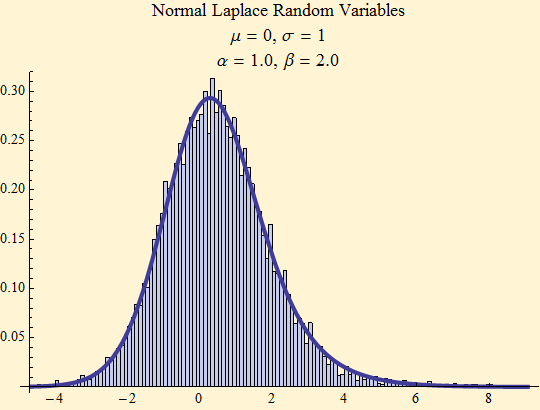
In the next section we will look at the double Pareto-lognormal distribution.

© Copyright 2007 mathestate    Fri 28 Dec 2007