DoubleParetoLogNormal

Double Pareto - Log Normal Distribution

In the last section we derived a normal Laplace distribution as the convolution of the difference of two exponential random variables and a normal random variable. Next we take the exponent of this random variable to obtain a new distribution that has the same relation to the normal Laplace distribution as the log normal distribution has to the normal distribution. Thus the density function becomes:

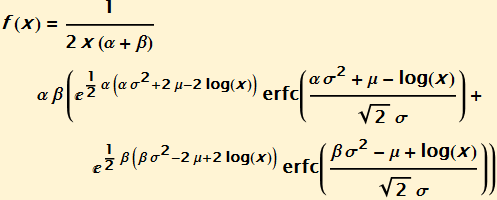
And the distribution function is:

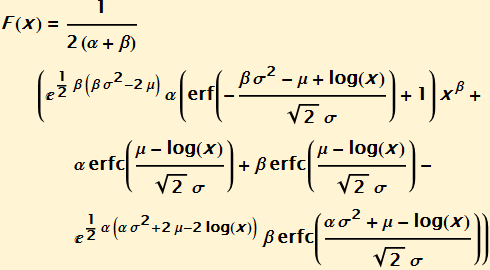
Random variables can be easily generated by taking the exponent of a normal-Laplace random variable which is the convolution of a normal random variable with the difference of two exponential random variables.

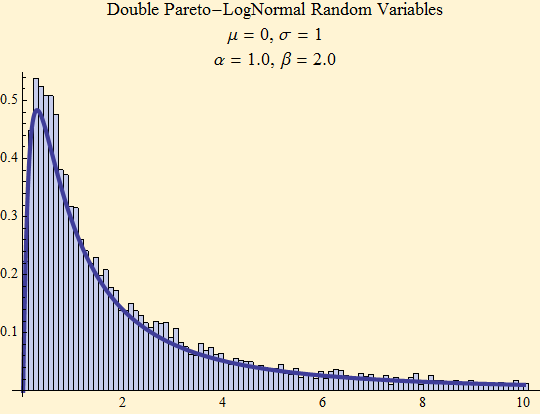
Graphics:Double Pareto-LogNormal Random Variables μ = 0, σ = 1 α = 1.0, β = 2.0

The log- log plots of the distribution function for the above parameters show the tails to be log-linear.

Graphics:Log-Log Plot Right Tail: 1-F[x]

Graphics:Log-Log Plot Left Tail: F[x]

The theoretic importance of the distribution is that it can be derived as the solution to an Itô stochastic integral for geometric Brownian motion. The full proof is laid out in a paper by William Reed, The Pareto Law of Incomes - an Explanation and an Extension.

We will give only a graphical demonstration. If you have two independent random variables one distributed log normally and the other exponentially the joint distribution looks like this.

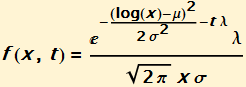
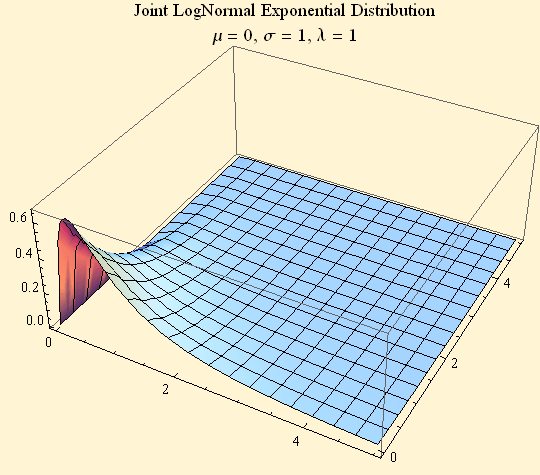
Graphics:Joint LogNormal Exponential Distribution μ = 0, σ = 1, λ = 1

For simplicity we will consider the case μ = 0. Now suppose that the Exponential process is stopped at time t = , the marginal distribution becomes:

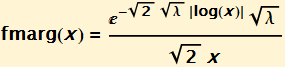
If we simplify this for x > 1 and 0 < x < 1, we get two distributions with Pareto tails.

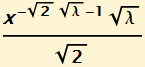
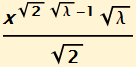
In summary the double Pareto - lognormal distribution has power tails and is consistent with a geometric Brownian motion that is generated with time process that is exponentially distributed and stopped. The general form of this distribution has a random variable that can be generated as the exponent of the sum of a normal random variable with the difference of two exponential random variables. It appears theoretically an ideal distribution to describe the structure of order books for the continuous double auction model of markets.