Continuous Double Auction Model,  Part II

On another page we developed a model of a continuous double auction, using a Pareto distribution to get the heavy tails in the order books.  We now update this with a double Pareto - log normal distribution to develop the price structure in the limit order books.  This distribution has power tails; if the right power tail has a tail exponent less than two, it and its negative relative will generate a heavy tailed order book structure.

We do a demonstration of the price structure of order books, assuming a double Pareto - log normal random variable is responsible for logarithmic differences in prices.

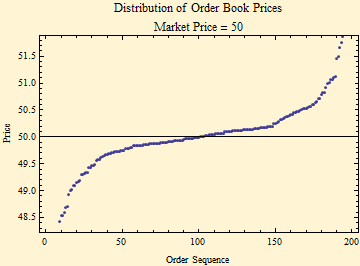
Just like the previous example we do a run of 10,000 matching intervals.  Only unmatched orders mktnet are considered in this version.  Matched orders don't change the price in the model.  lmtlen needs to be closely matched to the maximal expected absolute values of mktnet or the fat-tails won't occur.  The Mathematica algorithm is shown below.

A plot of all the prices.

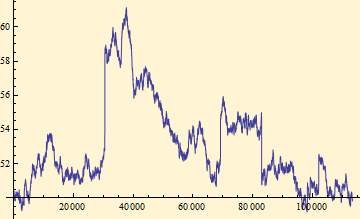
Sum the log returns of prices at intervals of 50 prices then calculate stable parameters of summed log returns.

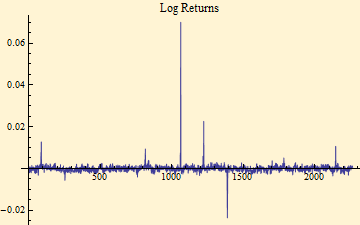
The system outputs true stable tails, as expected by the generalized central limit theorem.

Stable parameters
{1.83232, 0.0879309, 0.000718454, -0.0000494793}

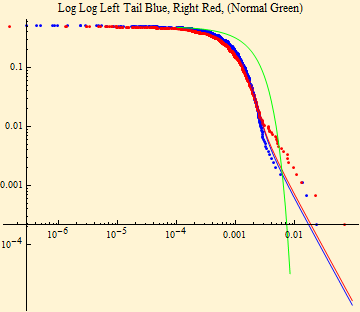
We have created a simple model of a continuous double auction.  It has heavy tails generated by a double Pareto - log normal distribution, sums of random variables from such a heavy tailed distribution converge to a stable distribution.

© Copyright 2008 mathestate    Mon 12 May 2008