Complex Numbers and the Stable Characteristic Function.
Where z is complex and r, θ, u, and v are Real, z can be represented in polar and Cartesian forms:
![]()
Expanding the polar form.
![]()
Therefore,
![]()
Absolute values
![]()
Argument
![]()
Conjugate
![]()
The stable characteristic function, 1 - parameterization
![]()
This can be rewritten in polar complex form
![]()
Thus
![]()
![]()
The Quick approximation of stable γ, using empirical characteristic function, ecf, where ![]() is each random variable uses the absolute value of the characteristic function.
is each random variable uses the absolute value of the characteristic function.
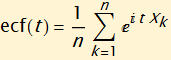
If ![]() is from a stable distribution then
is from a stable distribution then
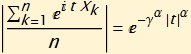
Letting t = 1,
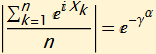
Since stable distributions are scalable, if we divide each ![]() by γ the scaled stable characteristic function will have γ = 1 and
by γ the scaled stable characteristic function will have γ = 1 and
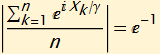
In Mathematica this can be rewritten and solved numerically:
![]()
Thus γ can be approximated numerically from the empirical characteristic function independently of α for any stable distribution including the normal distribution. This is how we approximate market volatility, using a small enough sample over which γ hasn't changed much.

© Copyright 2009 mathestate Sat 21 Feb 2009
