The Variance - One Measure of Risk
Below is a case with the same expectation but less dispersion. In common English and in formal statistical meaning, the area under the curve represents the variance from the expectation. This may be viewed as how likely or unlikely it is that our expectations will be met. The curve below indicates that all the possible outcomes are closer to the expectation, thus the variance [risk] is less here than for the prior curve.
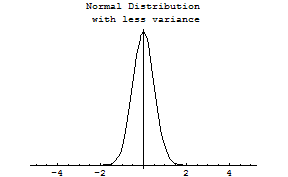
These two curves have been created using the mathematics of the famous "bell curve", also known as the normal distribution. As important and powerful as these mathematics are, they have limitations. Several properties of the normal distribution make its use questionable for financial applications. First, it is symmetrical, meaning that there must be an equal number of outcomes on either side of the mean (another term for the expectation). Second, it rapidly descends to the x-axis creating something that statisticians refer to as a particular kind of "asymptotic behavior". This rapid decline precludes finding or considering a large number of outcomes of any size or a small number of large outcomes that are located far from the expectation. Such things are known as "extreme values". Another way of saying this is that the normal distribution is "compact" around the mean. All observations
must be within a certain range of the mean for the normal distribution to accurately represent reality.


