The Cumulative Distribution Function (CDF)
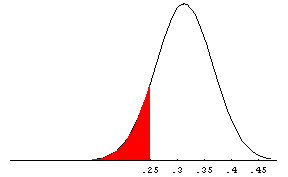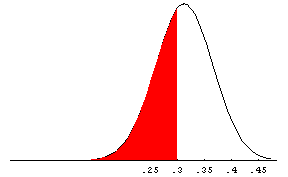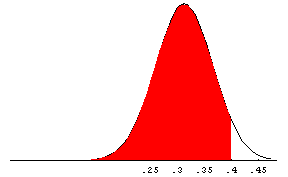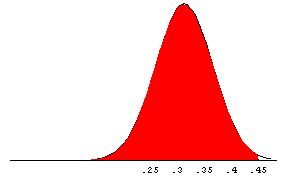
A companion and equally important tool is a Cumulative Distribution Function (CDF) that permits us to calculate the portion of the distribution that is contained under just a fraction of the pdf. The practical meaning of this is to permit us to compute probabilities of particular events. Continuing to believe that our distribution is normal, we can, using the CDF, calculate the probability that any specific reported expense ratio will occur. In the table to the right of the pdf we see that when the portion highlighted in red is to the left of .25 on the x axis, that portion constitutes 8.398% of the area under the curve. So, based on that value or one lower occuring about 8.4% of the time, we conclude that there is about an 8.4% chance that an EVR of .25 is correct.
 |
|
