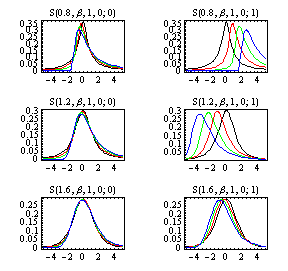
Parameterization of Stable Laws
The S(α, β, γ, δ; 0) parameterization is the best choice for numerical computation of stable distributions, since it has the simplest form for the characteristic function that is continuous in all four parameters. The S(α, β, γ, δ; 1) has been commonly used in economic literature and has the property that the location parameter, δ, is the mean when α > 1. The graphics array below demonstrates these two parameterizations. The scale parameter, γ, has been set to 1 and the location parameter, δ is 0. Each graph shows varying values of β {0, 1/3, 2/3, 1} in {black, red, green, blue} colors respectively at the value of α and type listed on the graph. Negative values of β would give mirror image graphs. When α is near 1, the mode in the S(α, β, γ, δ; 1) parameterization moves dramatically; the S(α, β, γ, δ; 0) parameterization progressively reduces this motion as alpha approaches one.