Using Stable Distributions in Mathematica
The StableRandom generator makes it easy to experience the behavior of stable distributions. Below three stable random samples are generated. Note how extreme outliers may be for lower values of alpha. A stable sample with α = 2 has the same dispersion as the normal distribution. α = 1.7 is typical of stock price returns.

The Stable MathLink Package also has data analysis capability and can perform a maximum likelihood fit to data in a variety of parameterizations. It contains a very fast StableQkPDF routine that makes maximum likelihood fitting possible for large sample sizes. The StableMLFit function provides a maximum likelihood fit to the data. The S(α, β, γ, δ; 1) parameterization is used in the example.
p1 = {1.3, 0.9, 1, -0.5}
s4 = StableRandom[1000,p1,1];
p2 = StableMLFit[s4, 1]
{1.28128, 0.885552, 1,00845, -0.370614}
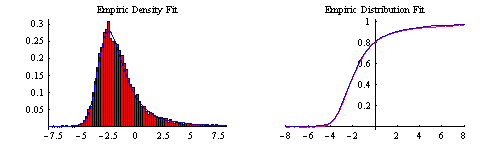
The graphs below compare the fits to the empiric density and distribution of the sample.
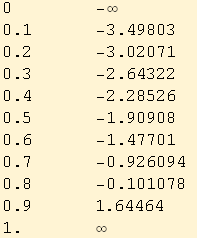
The StableQuantile function can be used to print a table of cumulative probabilities for the data set in the above example.