A Graphic Comparison
How much does this matter? The answer is: It depends. The left graphic below shows the normal (red) and a right skewed heavy tail (green) distribution. The graphic on the right enlarges the right tail section of the left graphic. The amount of difference depends on what you are measuring, the importance of accuracy and what part of the distribution is of greatest interest. If one views risk as variation from the mean, it is clear that the Stable distribution - because it permits extreme values - reveals more about the variation than the normal. Stated differently, the assumption of normality has the effect of blinders. It restricts one's view of extreme values.
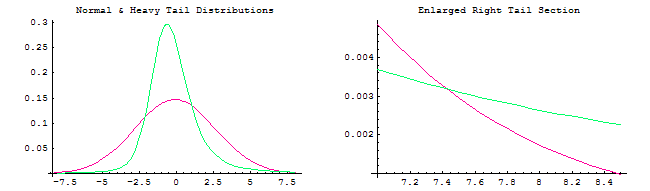
Using the Cumulative Distribution function has we have previously, we can calculate how much probability mass is under the different curves. For the right tail, because the scale (y axis values) is very small, the probability differences are small. One must be measuring very small variation and require high accuracy for the difference in probability to be important. But that is not so for the center of the distribution.
