Is the Stable Frontier "Efficient"?
One learns in school that Modern Portfolio Theory offers "gains from diversification", the mathematics of not putting all your eggs in one basket. An extension of that notion is the so-called "Efficient Frontier", a sidewise parabolic curve the upper half of which represents the way one can optimize return while minimizing risk. The farthest left point of that curve, the "nose" of the bullet-shaped parabola represents the "minimum variance portfolio". As we have seen, the assumption of normality - key to efficient set mathematics - understates risk. Thus it would seem likely that if returns are distributed non-normal stable, as real estate returns appear to be, the minimum variance real estate portfolio has greater risk than theory predicts.
Below five pairs of efficient frontiers cycle and repeat in the graph. Each pair represents two portfolios, one composed of three assets drawn from a non-normal, stable sample (where alpha = 1.4, a value common to private real estate return distributions); the other assumes the sample is distributed normally (where alpha = 2).
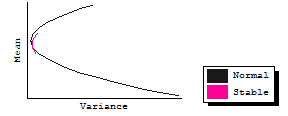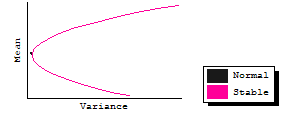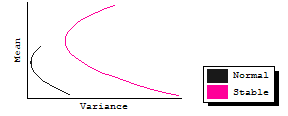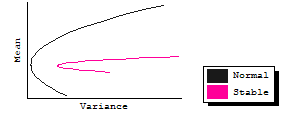
Notice several things as the graphic rotates through the five cases. First, the upper half (the only part we care about) of the non-normal frontier always plots behind (to the right of) the normal frontier, meaning that - not surprisingly - there is more variance. Second, there is a considerable difference in the scale of the two plots. For one of the cases the normal frontier is a mere dot, barely visible just to the left of the nose of the stable plot. Thus, not only in that case is there more risk but the range of returns is much greater for the non-normal stable case.
What have we learned from this? One lesson is that the power of mathestate is unrestrained by the assumption of normality.
